2.3 组织并行线程

【CUDA 基础】2.3 组织并行线程

2018-03-09 | CUDA ， Freshman | 0 |

Abstract: 本文介绍CUDA模型中的线程组织模式 Keywords: Thread，Block，Grid

组织并行线程

2.0 CUDA编程模型中我们大概地介绍了CUDA编程的几个关键点，包括内存、kernel，以及今天我们要讲的线程组织形式。2.0中还介绍了每个线程的编号是依靠块的坐标（blockIdx.x等）、网格的大小（gridDim.x等）、线程编号（threadIdx.x等）、线程的大小（blockDim.x等）来确定的。

这一篇我们就详细介绍每一个线程是怎么确定唯一的索引，然后建立并行计算，并且不同的线程组织形式是怎样影响性能的：

• 二维网格二维线程块
• 一维网格一维线程块
• 二维网格一维线程块

使用块和线程建立矩阵索引

多线程的优点就是每个线程处理不同的数据计算，那么怎么分配好每个线程处理不同的数据，而不至于多个不同的线程处理同一个数据，或者避免不同的线程无组织地访问内存。如果多线程不能按照组织合理地工作，那么就无法发挥并行计算的优势，必须有组织、有规则的计算才有意义。

我们的线程模型前面2.0中已经有个大概的介绍，但是下图可以非常形象地反映线程模型，不过注意硬件实际的执行和存储不是按照图中的模型来的，大家注意区分：

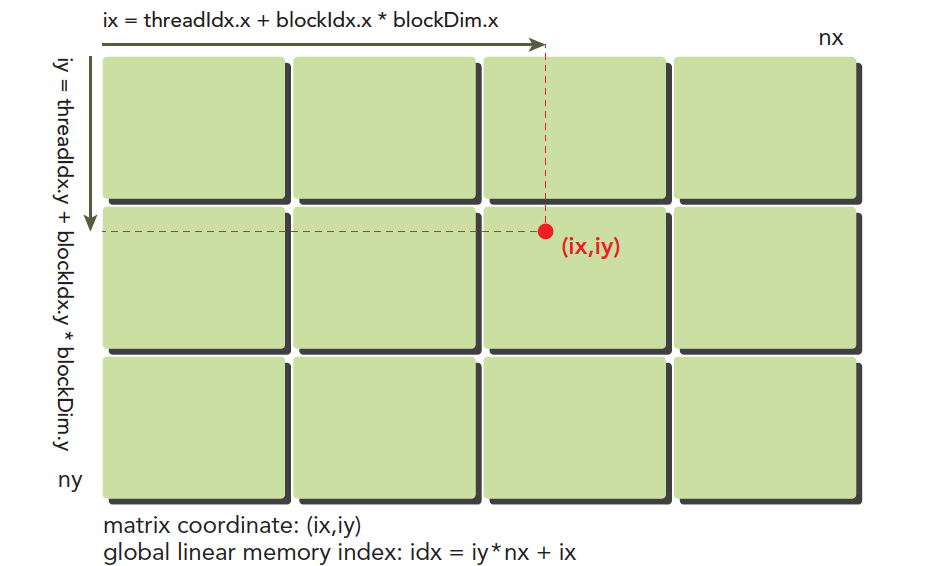
这里(ix,iy)就是整个线程模型中任意一个线程的索引，或者叫做全局坐标，局部坐标当然就是(threadIdx.x,threadIdx.y)了，当然这个局部坐标目前还没有什么用处，它只能索引线程块内的线程，不同线程块中有相同的局部索引值，比如同一个小区，A栋有16楼，B栋也有16楼，A栋和B栋就是blockIdx，而16就是threadIdx。

图中的横坐标就是：

ix = threadIdx.x + blockIdx.x × blockDim.x

纵坐标是：

iy = threadIdx.y + blockIdx.y × blockDim.y

这样我们就得到了每个线程的唯一标号，并且在运行时kernel是可以访问这个标号的。前面讲过CUDA每一个线程执行相同的代码，也就是异构计算中说的多线程单指令，如果每个不同的线程执行同样的代码，又处理同一组数据，将会得到多个相同的结果，显然这是没意义的。为了让不同线程处理不同的数据，CUDA常用的做法是让不同的线程对应不同的数据，也就是用线程的全局标号对应不同组的数据。

设备内存或者主机内存都是线性存在的，比如一个二维矩阵(8×6)，存储在内存中是这样的：

我们要做管理的就是：

• 线程和块索引（来计算线程的全局索引）
• 矩阵中给定点的坐标(ix,iy)
• (ix,iy)对应的线性内存的位置

线性位置的计算方法是：

idx = ix + iy × nx

我们上面已经计算出了线程的全局坐标，用线程的全局坐标对应矩阵的坐标，也就是说，线程的坐标(ix,iy)对应矩阵中(ix,iy)的元素，这样就形成了一一对应，不同的线程处理矩阵中不同的数据。举个具体的例子，ix=10,iy=10的线程去处理矩阵中(10,10)的数据，当然你也可以设计别的对应模式，但是这种方法是最简单、出错可能最低的。

我们接下来的代码来输出每个线程的标号信息：

#include <cuda_runtime.h>
#include <stdio.h>
#include "freshman.h"

__global__ void printThreadIndex(float *A, const int nx, const int ny)
{
    int ix = threadIdx.x + blockIdx.x * blockDim.x;
    int iy = threadIdx.y + blockIdx.y * blockDim.y;
    unsigned int idx = iy * nx + ix;
    printf("thread_id(%d,%d) block_id(%d,%d) coordinate(%d,%d) "
           "global index %2d ival %2d\n", threadIdx.x, threadIdx.y,
           blockIdx.x, blockIdx.y, ix, iy, idx, A[idx]);
}

int main(int argc, char** argv)
{
    initDevice(0);
    int nx = 8, ny = 6;
    int nxy = nx * ny;
    int nBytes = nxy * sizeof(float);

    // Malloc
    float* A_host = (float*)malloc(nBytes);
    initialData(A_host, nxy);
    printMatrix(A_host, nx, ny);

    // cudaMalloc
    float *A_dev = NULL;
    CHECK(cudaMalloc((void**)&A_dev, nBytes));

    cudaMemcpy(A_dev, A_host, nBytes, cudaMemcpyHostToDevice);

    dim3 block(4, 2);
    dim3 grid((nx - 1) / block.x + 1, (ny - 1) / block.y + 1);

    printThreadIndex<<<grid, block>>>(A_dev, nx, ny);

    CHECK(cudaDeviceSynchronize());
    cudaFree(A_dev);
    free(A_host);

    cudaDeviceReset();
    return 0;
}

这段代码输出了一组我们随机生成的矩阵，并且核函数打印自己的线程标号，注意，核函数能调用printf这个特性是CUDA后来加的，最早的版本里面不能printf，输出结果：

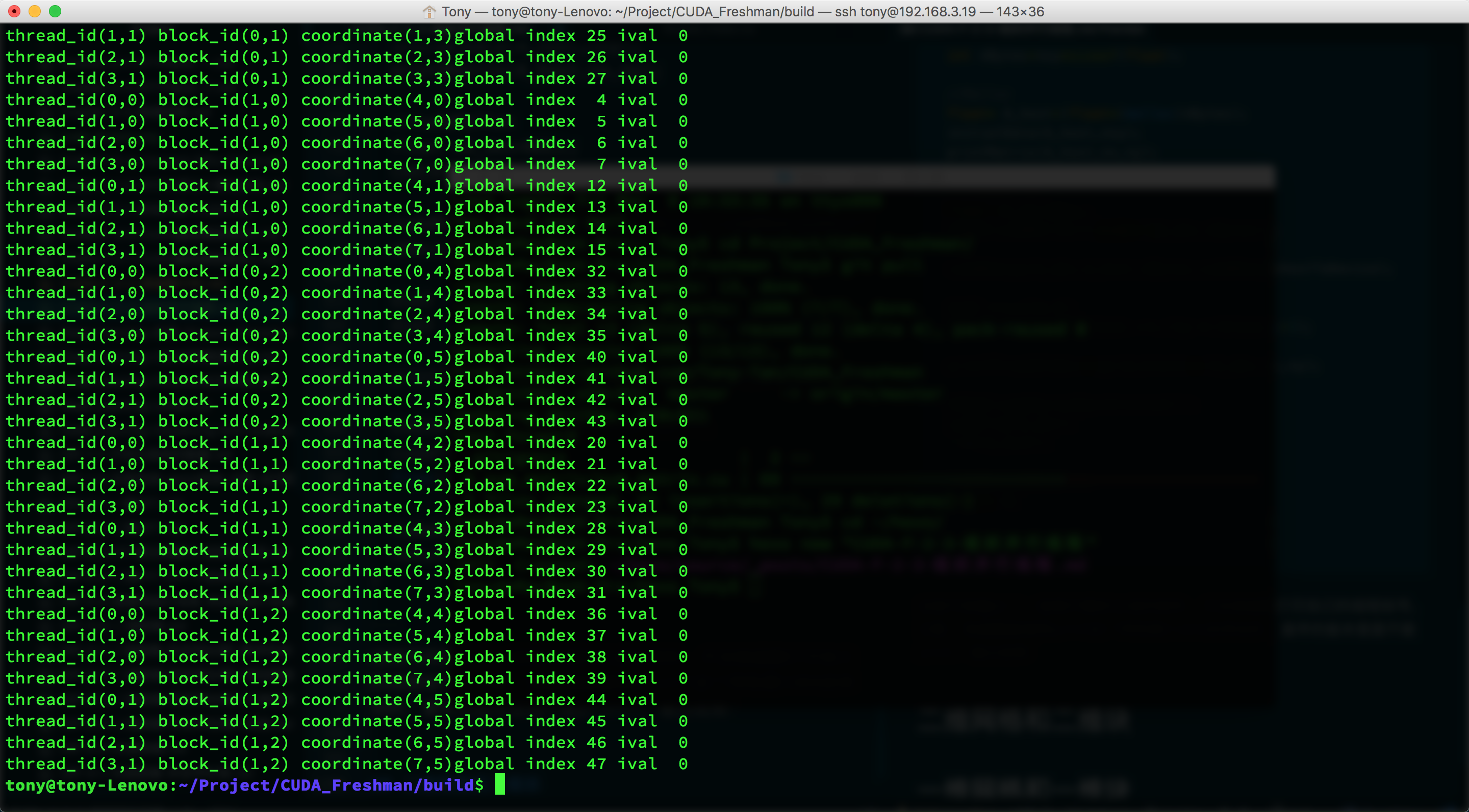
由于截图不完全，上面有一段打印信息没贴全，但是我们可以知道每一个线程已经对应到了不同的数据，接着我们就要用这个方法来进行计算了，最简单的当然就是二维矩阵加法。

二维矩阵加法

我们利用上面的线程与数据的对应完成了下面的核函数：

__global__ void sumMatrix(float * MatA, float * MatB, float * MatC, int nx, int ny)
{
    int ix = threadIdx.x + blockDim.x * blockIdx.x;
    int iy = threadIdx.y + blockDim.y * blockIdx.y;
    int idx = ix + iy * nx;
    if (ix < nx && iy < ny)
    {
        MatC[idx] = MatA[idx] + MatB[idx];
    }
}

下面我们调整不同的线程组织形式，测试一下不同的效率并保证得到正确的结果。什么时候得到最好的效率是后面要考虑的，我们要做的就是用各种不同的线程组织形式得到正确结果。

二维网格和二维块

首先来看二维网格二维块的代码：

// 2d block and 2d grid
dim3 block_0(dimx, dimy);
dim3 grid_0((nx - 1) / block_0.x + 1, (ny - 1) / block_0.y + 1);
iStart = cpuSecond();
sumMatrix<<<grid_0, block_0>>>(A_dev, B_dev, C_dev, nx, ny);
CHECK(cudaDeviceSynchronize());
iElaps = cpuSecond() - iStart;
printf("GPU Execution configuration<<<(%d,%d),(%d,%d)>>> Time elapsed %f sec\n",
       grid_0.x, grid_0.y, block_0.x, block_0.y, iElaps);
CHECK(cudaMemcpy(C_from_gpu, C_dev, nBytes, cudaMemcpyDeviceToHost));
checkResult(C_host, C_from_gpu, nxy);

运行结果：

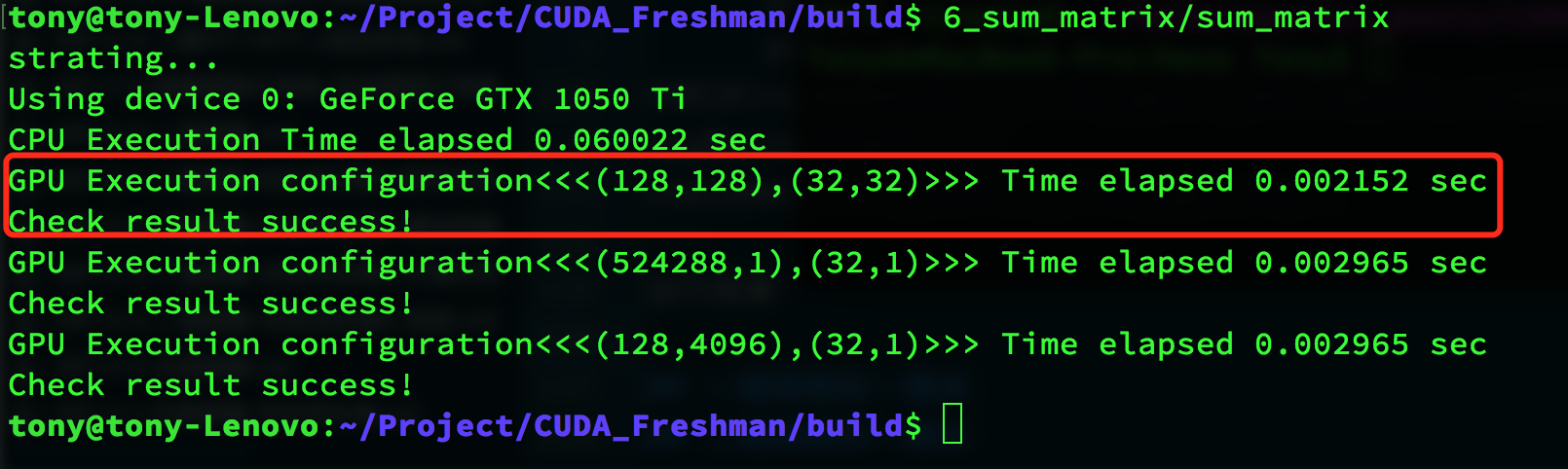
红色框内是运行结果，用CPU写一个矩阵计算，然后比对结果，发现我们的运算结果是正确的，用时0.002152秒。

一维网格和一维块

接着我们使用一维网格一维块：

// 1d block and 1d grid
dimx = 32;
dim3 block_1(dimx);
dim3 grid_1((nxy - 1) / block_1.x + 1);
iStart = cpuSecond();
sumMatrix<<<grid_1, block_1>>>(A_dev, B_dev, C_dev, nx * ny, 1);
CHECK(cudaDeviceSynchronize());
iElaps = cpuSecond() - iStart;
printf("GPU Execution configuration<<<(%d,%d),(%d,%d)>>> Time elapsed %f sec\n",
       grid_1.x, grid_1.y, block_1.x, block_1.y, iElaps);
CHECK(cudaMemcpy(C_from_gpu, C_dev, nBytes, cudaMemcpyDeviceToHost));
checkResult(C_host, C_from_gpu, nxy);

运行结果：

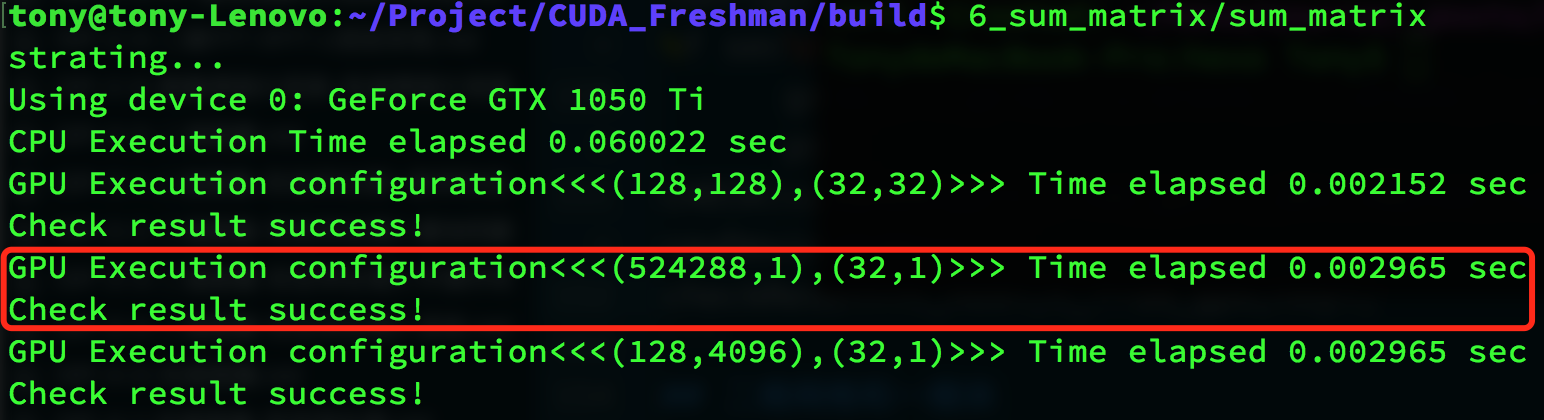
同样运行结果是正确的。

二维网格和一维块

二维网格一维块：

// 2d grid and 1d block
dimx = 32;
dim3 block_2(dimx);
dim3 grid_2((nx - 1) / block_2.x + 1, ny);
iStart = cpuSecond();
sumMatrix<<<grid_2, block_2>>>(A_dev, B_dev, C_dev, nx, ny);
CHECK(cudaDeviceSynchronize());
iElaps = cpuSecond() - iStart;
printf("GPU Execution configuration<<<(%d,%d),(%d,%d)>>> Time elapsed %f sec\n",
       grid_2.x, grid_2.y, block_2.x, block_2.y, iElaps);
CHECK(cudaMemcpy(C_from_gpu, C_dev, nBytes, cudaMemcpyDeviceToHost));
checkResult(C_host, C_from_gpu, nxy);

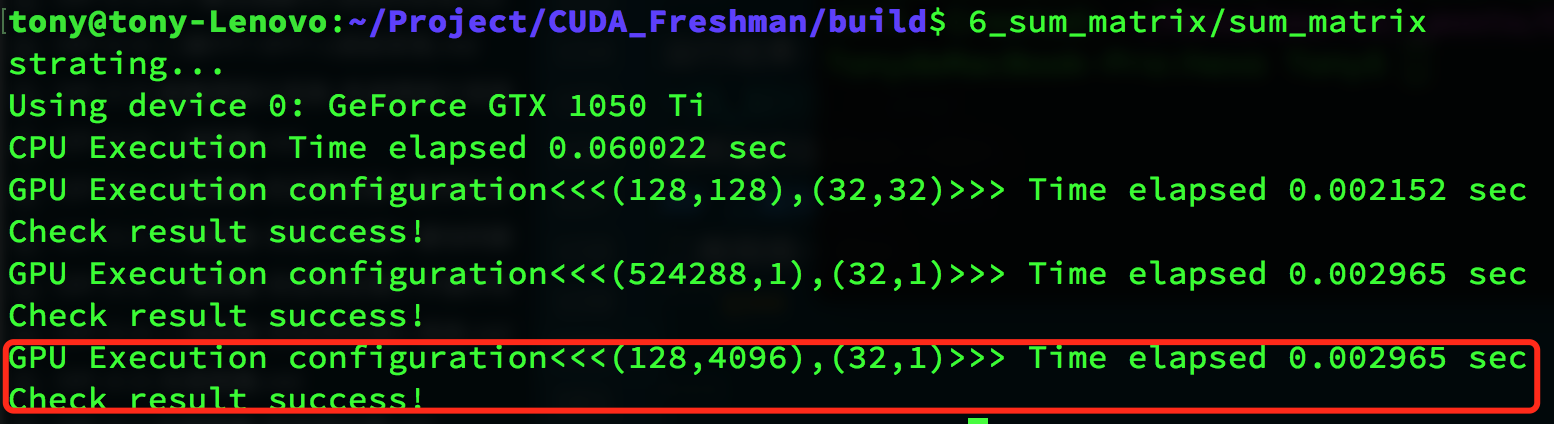
运行结果：

总结

用不同的线程组织形式会得到正确结果，但是效率有所区别：

线程配置	执行时间
CPU单线程	0.060022
(128,128),(32,32)	0.002152
(524288,1),(32,1)	0.002965
(128,4096),(32,1)	0.002965

观察结果没有多大差距，但是明显比CPU快了很多，而且最主要的是我们本文用不同的线程组织模式都得到了正确结果，并且：

• 改变执行配置（线程组织）能得到不同的性能
• 传统的核函数可能不能得到最好的效果
• 一个给定的核函数，通过调整网格和线程块大小可以得到更好的效果

第三章的执行模型，我们才会深入到硬件层面，追寻影响效率的根本原因。

代码库中有完整代码：https://github.com/Tony-Tan/CUDA_Freshman